Una secuencia para la introducción de la función cuadrática a través de la resignificación de aspectos variacionales

Una secuencia para la introducción de la función cuadrática a través de la resignificación de aspectos variacionales

A Sequence for Introducing the Quadratic Function through the Resignification of Variational Aspects

Uma sequência para introdução da função quadrática através de uma nova significação de aspectos variacionais

Octavio Augusto Briceño¹
Gabriela Buendía Ábalos²

¹ Estudiante de maestría del Instituto Politécnico Nacional Centro de Investigaciones en Ciencia Aplicada y Tecnología Avanzada, Cicata. México. Correo electrónico: octavioco11@gmail.com
² Profesora-investigadora de la Red de Centros de Investigación en Matemática Educativa Cimates. Correo electrónico: buendiag@hotmail.com

Resumen

Esta investigación gira alrededor de secuencias en las que la práctica de modelación se introduce en forma intencional y de esta manera se favorece en los estudiantes un aprendizaje significativo de la función cuadrática y sus aspectos variacionales. El trabajo es propuesto y aplicado a estudiantes de inicios del bachillerato (12-13 años). La investigación se fortalece gracias a las contribuciones que se obtienen al usar la metodología de experimentos de diseño. El marco teórico que sustenta el trabajo es la socioepistemología.

Palabras clave: Modelación, función cuadrática, socioepistemología, aspectos variacionales, experimentos de diseño.

Abstract

This research revolves around sequences, where the practice of modeling is introduced intentionally and thus is conducive to students learning about a significant quadratic function and its variational aspects. The work is proposed and applied to early high school students (12-13 years). The research is strengthened by the contributions that are obtained by using the methodology of design experiments. The theoretical framework underpinning the work is socioepistemology.

Keywords: Modeling, quadratic function, socioepistemology, variational aspects, design experiments.

Resumo

Esta pesquisa tem a ver com sequências, nas quais as práticas de modelagem são introduzidas de forma intencional e desta maneira favorece-se nos alunos a aprendizagem significativa da função quadrática e seus aspectos variacionais. O trabalho é proposto e implementado com alunos de ensino fundamental (12-13 anos). A pesquisa é fortalecida conforme as contribuições que são constituídas no uso da metodologia de experimentos de desing. O referencial teórico que fundamenta o artigo é a socioepistemologia.

Palavras chave: Modelagem, função quadrática, socioepistemologia, aspectos variacionais, experimentos de desing.

Introducción

Dentro de la investigación que sustenta este escrito se acoge la modelación como una práctica que ofrece las herramientas necesarias para establecer un vínculo entre contextos extra-escolares y los libros de texto junto con el discurso matemático escolar. Modelar significa dar una relación significativa y articulada entre elementos de ambos mundos. Se pretende dar a conocer secuencias de aprendizaje en las que la modelación resignifica la función cuadrática para estudiantes que inician el trasegar en el precálculo. Se favorece la articulación entre el conocimiento científico (fenómeno físico de movimiento) y el conocimiento escolar (gráficas cartesianas) por medio del desarrollo de argumentos y herramientas variacionales que fomentan nuevos significados.

La resignificación es la construcción del conocimiento mismo que hacen los individuos a la luz del desarrollo intencional de ciertas prácticas, como la modelación, y que está normado por aspectos institucionales y colectivos. Se manifiestan en el uso del conocimiento en una situación específica; en nuestro caso es el enriquecimiento, la articulación e integración de nuevos significados dados por los estudiantes al concepto de función cuadrática, la cual está mediada por aspectos variacionales a través del uso de gráficas y tablas.

El uso de las gráficas que las secuencias buscan favorecer lleva a que el estudiante reconozca puntos clave e intervalos en ellas, que permitirán reconocer el comportamiento variacional del fenómeno tratado; esto es, desarrollar argumentos a través de los cambios y variaciones que pueden sufrir las variables para determinar si el comportamiento es curvo o lineal. El uso de tablas numéricas propicia un manejo visual y significativo del sistema numérico, al tiempo que permite organizar la información y mostrar proporcionalidad entre las variables que intervienen, aspectos que apoyan en la resignificación de lo cuadrático y lineal.

Los experimentos de diseño darán la pauta para el desarrollo de las actividades en las secuencias. Confrey (2006) comenta, con relación a las investigaciones de diseño, que se busca documentar qué recursos y conocimientos previos ponen en juego los estudiantes en las tareas, cómo interactúan alumnos y profesores, cómo se crean las anotaciones y los registros, cómo brotan y evolucionan las nociones, qué recursos se usan y cómo se lleva a cabo la enseñanza a lo largo de la instrucción. Los experimentos de diseño que guiarán los aspectos metodológicos de la investigación.

Antecedentes

La función cuadrática ha sido objeto de estudio para muchos investigadores, en especial en la última década, cuando se ha ampliado el campo de acción en diferentes postulaciones. Hay estudios que se centran en encontrar secuencias que ayuden al aprendizaje y se enfoquen en él. Pech y Ordaz (2010), por ejemplo, muestran una secuencia didáctica para la enseñanza de la función en estudiantes universitarios, utilizando la metodología de ingeniería didáctica en un contexto socioepistemológico, en el cual el estudiante construye conocimiento matemático referente al concepto de función, en situaciones variacionales. Mercado, Aguas y Arrieta (2010) nos muestran a través de una secuencia didáctica la comprensión del concepto de función usando situaciones del contexto sociocultural en la práctica de modelación, aplicando un diagnóstico inicial para establecer estrategias didácticas. Estas investigaciones dan cuenta de la necesaria articulación para el conocimiento de la función cuadrática que se debe dar entre el fenómeno presentado y al representar sus variables en una gráfica. Se busca que por medio de esa articulación se llegue a la resignificación de un concepto.

Cordero y Suárez (2005) realizaron una investigación para resignificar la parábola mediante gráficas. Se utiliza un contexto físico para que el estudiante plasme los datos de las variables del fenómeno en una gráfica. Para los autores, la graficación es el medio por el cual la relación modelación-graficación-tecnología se puede implementar en las aulas para construir significativamente conocimiento matemático. En nuestra investigación proponemos que los estudiantes utilicen la graficación como el medio para generar argumentos sobre los aspectos variacionales involucrados y tener un conocimiento significativo de la función cuadrática durante la introducción académica del tema.

Villa (2008) considera que para lograr un mejor conocimiento del concepto de función cuadrática desde la perspectiva variacional hay que tener en cuenta aspectos como la relación entre dos magnitudes, llevar los datos a una tabla, identificar la razón de cambio entre las magnitudes, reconocer la variabilidad de la razón de cambio y comprender la función como un modelo.

Retomaremos entonces los aspectos variacionales mencionados en dichas investigaciones como base de los diseños que se experimentarán.

La modelación con enfoque socioepistemológico

Para Cantoral y Farfán (2003) la socioepistemología es el eje de investigación del pensamiento matemático y el lenguaje variacional. El énfasis para explicar la construcción de conocimiento matemático está en las prácticas sociales, que adquieren sentido en el campo de la variación y del cambio en los diferentes sistemas educativos. La socioepistemología como teoría permite mirar la educación matemática no solo como transmisión de conocimientos, en la que se expresan postulados, se solucionan problemas, se realizan demostraciones, sino que permite mirar más allá de los conceptos, cuál es su trasfondo, cómo es que la práctica norma su generación para permitir transformar y llevar los conceptos a otros contextos, acercándonos al mundo real. Para Buendía y Montiel (2011) la socioepistemología se constituye como un enfoque teórico para comprender los fenómenos específicos que se relacionan con la transmisión de conocimiento matemático, reconociendo su naturaleza social a través del papel epistemológico que se le asignan a las prácticas sociales como normativas de ese conocimiento matemático.

Los trabajos enmarcados en la socioepistemología no coinciden en los conceptos, pero sí en las prácticas que lo anteceden y que se manifiestan en un contexto sociocultural específico. Importa cómo se usa el conocimiento en ese contexto, la manera en que se construye, qué razonamientos se asocian y qué clase de significados se comparten. La modelación en un marco socioepistemológico permite que los estudiantes resignifiquen conceptos matemáticos con base en el conocimiento matemático. Esto lo podemos observar en la investigación de Córdoba (2011), quien nos muestra la práctica de modelación en un marco socioepistemológico, tratando el fenómeno de enfriamiento de Newton y usando la ecuación diferencial de primer orden como conocimiento matemático aplicado a estudiantes de nivel ingenieril. Esto le permite hablar de la resignificación de una ecuación diferencial favorecida por una práctica, la modelación, en un contexto específico como la ingeniería.

La investigación

En muchas ocasiones escolares se utiliza la modelación para enseñar a modelar, para enseñar teoría, como herramienta didáctica o para medir un objeto matemático simplemente. En esta investigación se reconoce la modelación en un acercamiento socioepistemológico como práctica que permite desarrollar actividades didácticas teniendo en cuenta la epistemología de lo cuadrático, la parte cognitiva de los individuos involucrados, los elementos didácticos propios del contexto escolar y social en el cual se desarrollan las actividades propuestas; lo anterior reconociendo el papel de la argumentación e interacción de los estudiantes como herramienta.

En las actividades desarrolladas intervienen elementos de la cotidianidad del estudiante, la experimentación, las diferentes relaciones entre el conocimiento científico y el conocimiento escolar, para resignificar y elaborar así procesos de conocimiento matemático en el aula, con relación a aspectos variacionales de la función cuadrática.

A través de la modelación se espera que el individuo fundamente el saber hacer en contexto y genere significados para el conocimiento matemático. Este conocimiento se concibe no en función de la adquisición del concepto de "función cuadrática" sino en la generación de significados a través de la práctica de modelación; por ello se habla de resignificación.

La investigación se dirige a crear ambientes ricos en significados y en argumentos, partiendo de cada una de las acciones de los individuos como seres humanos en las actividades matemáticas trazadas. La modelación norma el quehacer de los estudiantes y favorece así el desarrollo de herramientas que queremos en ellos, para que lleguen a obtener el conocimiento de la manera acertada y práctica.

Los experimentos de diseño son la metodología seleccionada para desarrollar lo anterior ya que permiten concebir los diseños, no como tareas de clase, sino dentro de un diseño pedagógico mirado hacia el aula de una manera inteligente y propositiva a partir de resultados de la investigación, lo cual permite además desarrollar teoría. Lo anterior nos lleva a analizar cómo los aspectos variacionales pueden vivir en el aula de clase con los estudiantes.

Aspectos variacionales

Los aspectos variacionales en el estudio de la función cuadrática se establecen como elementos de análisis en el desarrollo de la investigación. Cada uno de estos aspectos y el conjunto de ellos encierran el objetivo de la investigación: discutir cómo la modelación favorece los aspectos variacionales en los fenómenos físicos presentados en las secuencias. Los aspectos variacionales por reconocer en el análisis de investigación y que conforman nuestra malla de análisis son los siguientes: el papel del tiempo como variable independiente; el uso de las gráficas en el reconocimiento significativo de puntos claves y los intervalos como parte fundamental en el contexto variacional; y el uso de tablas en las que la secuencia numérica se relaciona con lo variacional.

La modelación y los aspectos variacionales establecen un dúo bastante productivo. Briceño (2014) comenta que los aspectos variacionales en la función cuadrática se resignifican mediante la práctica de modelación, porque a través de ella se puede determinar cómo se pone en juego el conocimiento matemático en forma de herramienta, qué relaciones se utilizan, por qué camino se dirige, el para qué del conocimiento.

Tiempo como variable independiente

El tomar fenómenos físicos para el estudio de la variabilidad de la función cuadrática implica reconocer el tiempo como variable independiente para analizar la variación de otro componente, como distancia o altura, al poner un objeto cualquiera en movimiento. Dolores, Alarcón y Albarrán (2002) comentan que las representaciones semióticas del movimiento utilizadas con frecuencia en cinemática hacen visibles las trayectorias en representación espacial, y en matemática escolar los datos y las variables se plasman en las gráficas cartesianas. Trabajos como el de Díaz (2005) reconocen el tiempo como algo connatural que tiene que ver con estados distintos de acuerdo al paso del tiempo, donde hay un antes y un después de una misma cosa a la que se le detectan estados diferentes.

Uso de la gráfica

El uso que se le puede dar a la gráfica en fenómenos de movimiento permite relaciones de una manera más coherente debido a la visualización del comportamiento del fenómeno tratado. Cuando se toman intervalos en una gráfica se pueden analizar trozos de ella, es decir volver más pequeños los trayectos, con el propósito de que el estudiante establezca las diferencias cuando se tiene una porción grande de la gráfica o cuando es pequeña. Buendía (2012) en su trabajo de investigación aplica dos talleres a profesores de matemáticas, en los cuales se plantea el problema que consiste en una gráfica cartesiana velocidad-tiempo que representa lo que sucede con dos ciclistas que se mueven a distintas velocidades. Se reconoce que es probable que para la solución de las actividades se use la gráfica para facilitar la consecución del logro y también se reconoce el uso de los intervalos en la gráfica como una estrategia de resolución de la actividad propuesta, en la cual la acumulación de distancias de intervalos da la proporción total y se puede transitar significativamente en la relación distancia-velocidad. También podemos pensar en nuestro caso que el estudiante, para esbozar la gráfica, utiliza el plano cartesiano con cuadrícula; este se transforma en pequeños intervalos constituidos que le permiten establecer intersecciones distancia-tiempo o altura-tiempo y uniendo dichas intersecciones mostrar el comportamiento gráfico del fenómeno tratado.

Tomar puntos clave facilita, además, la consecución de los intervalos de tiempo o distancia, porque estos permiten realizar interpretaciones y cálculos de movimiento del objeto. Buendía (2012) comenta que una estrategia de resolución cuando se plantean tareas a través de gráficas es identificar puntos clave o significativos, ya sea numéricamente para utilizarlos en fórmulas o de forma gráfica, para hallar las coordenadas de intersección. Estos puntos están ligados con los intervalos, porque estos últimos favorecen el tránsito de una concepción local-puntual del comportamiento en cuestión a una global.

Uso de tablas a través de una secuencia numérica

Las tablas favorecen la visualización de datos porque a partir de ellas se puede determinar el tipo de proporcionalidad que presentan las variables y en algunos casos el comportamiento del movimiento. El tomar intervalos de tiempo iguales permite observar en las tablas si la distancia o altura aumenta o disminuye en el transcurrir del tiempo. Arrieta (2003) llama numerización de los fenómenos a aquellas prácticas de modelación en las que se parte de la recolección de datos numéricos de un fenómeno y luego se realizan prácticas de predicción para construir así modelos numéricos.

Aspectos metodológicos

La metodología escogida para la aplicación de las secuencias son los experimentos de diseño. La investigación de diseño surge ante la necesidad de metodologías que permitan obtener argumentaciones basadas en la evidencia de contextos naturales, de abordar cuestiones teóricas sobre la naturaleza del aprendizaje en un determinado contexto y de producir resultados de investigación a partir de la evaluación formativa. La mayoría de los experimentos de diseño de aula se conceptualizan como casos del proceso de apoyo a los grupos de aprendizaje de los estudiantes en un dominio de contenido particular (Cobb et ál. 2003).

Nuestros aspectos metodológicos inician con la aplicación de un cuestionario diagnóstico para indagar qué conocimiento posee el estudiante referente a trayectorias, gráficas, relación distancia-tiempo y tratamiento de situaciones que reflejan la modelación como práctica. El instrumento se aplicó a estudiantes de entre 11 y 12 años. El cuestionario diagnóstico sirvió de punto de partida para el diseño y la aplicación de las secuencias y para reflejar el nivel de profundidad del conocimiento que estos estudiantes tienen sobre función y función cuadrática. Las secuencias se diseñan partiendo de fenómenos físicos extraídos de la observación diaria, en los que el estudiante puede establecer relaciones para el desarrollo de los aspectos variacionales elegidos de la función cuadrática.

El diseño de las secuencias se fortalece en el ámbito de lo cotidiano, es decir, en aquello que el estudiante puede observar y relacionar con su medio ambiente. Por esto se plantean dos secuencias relacionadas con el movimiento de ida y regreso de un auto y el lanzamiento vertical de una pelota. Cobb et ál. (2003) comentan que la mayoría de los experimentos de diseño de aula se conceptualizan como casos del proceso de apoyo a los grupos de aprendizaje de los estudiantes en un dominio de contenido particular.

Secuencia 1

La actividad se basa en el estudio del desplazamiento que sufre un automóvil de un punto determinado a otro. Su propósito es que el estudiante analice el movimiento de un objeto para que busque y encuentre las diferentes relaciones entre lo que ve y piensa y las plasme en el desarrollo de las preguntas propuestas. El auto parte del punto B y avanza hacia la derecha pasando por los puntos G, H, I; disminuye progresivamente la velocidad hasta detenerse en el punto C; luego regresa al sitio de partida aumentando progresivamente su velocidad hasta obtener la misma velocidad con la que partió y pasando por los mismos puntos. El fenómeno propuesto del movimiento se simula a través del software de GeoGebra como se muestra en la figura 1.

La secuencia consta de siete preguntas en las cuales se consideran los aspectos variacionales de la función cuadrática propuestos.

1. Si dos autos se ponen en movimiento al mismo instante, uno va en forma horizontal moviéndose de B-C a C-B y otro a través de una montaña, las distancias que recorren son las mismas y el tiempo transcurrido también es idéntico, ¿cómo serían sus trayectorias? Dibújelas. Se quiere llevar los puntos marcados en el movimiento de ida y regreso horizontal (B, G, H, I, C) al movimiento del auto en montaña. Discuta con sus compañeros dónde los localizaría. Márquelos.
2. Tomando el tramo B-G y el I-C de ida, al comparar los tiempos gastados en esos tramos, ¿cómo serían y por qué?
3. Si tomo esos mismos tramos pero de regreso C-I y G-B, ¿cómo sería la comparación de los tiempos con respecto al movimiento de ida?
4. Si le pidieran llevar el movimiento del auto F a una gráfica teniendo como magnitudes el tiempo y la distancia, ¿cómo lo haría? Esbócela.
5. Compare la gráfica que obtuvo con la de otros compañeros. ¿Qué diferencias encuentra?
6. Toma intervalos de tiempo pequeños en el movimiento que hace el auto de ida y regreso para medir las distancias recorridas y plasmarlas en una tabla, ¿cómo cree que es la relación de los datos numéricos del tiempo con relación a la altura? Comente.
7. ¿Cómo sería la gráfica del movimiento teniendo en cuenta la situación del numeral anterior? ¿Tiene alguna similitud con la que esbozó anteriormente? Compare la gráfica y dé su opinión.

Secuencia 2

En esta secuencia se presenta otra actividad también de movimiento, pero ahora en desplazamiento vertical: el lanzamiento de una pelota hacia arriba. La secuencia comienza presentando cómo sería el lanzamiento de la pelota (véase la figura 2). Para realizar el experimento se coloca un fondo especial con el fin de captar con mayor nitidez el movimiento del objeto lanzado. Para el análisis del fenómeno de lanzamiento vertical se utilizará el software Tracker-310 y el software Modellus, programas de libre acceso que ayudan a realizar modelaciones de este tipo de situaciones de movimiento.

La secuencia consta de siete preguntas, que se relacionan con los aspectos variacionales.

1. Realice los siguientes lanzamientos con una pelota: un lanzamiento vertical y uno que forme una curva. Suponga que se demoran los movimientos igual tiempo en caer y llegan a la misma altura. Comente con sus compañeros. Tomando unos puntos cualesquiera en el lanzamiento vertical, transportarlos al otro movimiento ¿dónde los ubicaría? Dibuje en una hoja las dos trayectorias y localice los puntos.
2. ¿Cómo llevaría a una gráfica el movimiento que hace la pelota al lanzarla verticalmente desde el punto de partida (P) hasta que llega nuevamente a su inicio?



3. Comente con sus compañeros el lanzamiento de la pelota hacia arriba un instante antes de que esta llegue al punto donde se regresa, y ese mismo intervalo de tiempo después de que se regresa. ¿Cómo serían las alturas en esos puntos y qué pasa con el tiempo transcurrido? ¿Por qué sucede eso?
4. Si tomamos un corto intervalo de tiempo después del lanzamiento y ese mismo momento de tiempo, pero antes de caer, ¿qué piensa sobre las alturas en ese intervalo y a qué se debe?

Para realizar la siguiente actividad los estudiantes toman una pelota y realizan un lanzamiento vertical hacia arriba. Con anterioridad se han marcado en una regleta valores numéricos con el propósito de medir las alturas en un determinado tiempo.

5. Tomando intervalos de tiempo pequeños, mida las alturas correspondientes y muéstrelas en una tabla. Deben ser más de diez tomas. ¿Cómo cree que es la relación de los datos numéricos del tiempo con respecto a la altura? Comente.
6. ¿Cómo sería la gráfica del movimiento teniendo en cuenta la situación del numeral anterior? ¿Tiene alguna similitud con la esbozada en el numeral 2? Comparen su gráfica con la obtenida por otros grupos y dé su opinión.
7. Si le piden comprobar que el modelo gráfico que se obtuvo es el indicado para el fenómeno mostrado de lanzamiento vertical, ¿qué debe hacer?

Planeación de las secuencias

Cada una de las secuencias se planea mirando aquellos fenómenos más cercanos a los estudiantes o que ellos presencian diariamente. Esto se logra dialogando con ellos e intercambiando ideas, hasta observar qué fenómenos conocen. Una vez que se tienen diseñadas las secuencias se eligen doce estudiantes y se subdividen en cuatro grupos a los cuales se aplica cada una de las actividades propuestas. A cada grupo en su lugar de trabajo se le proporcionó una grabadora de audio y un computador. Se posicionó una cámara de video en un lugar fijo, controlada por una persona y otra cámara rodante que tomó videos cortos y fotografías manejada por otra persona, a quien se le indicó en qué momentos o instantes debe realizar las tomas. Cobb et ál. (2003) sostienen que el apoyo tecnológico para la generación de los datos (por ejemplo, cámaras de video, sistemas de grabación de audio sofisticados, dispositivos electrónicos de almacenamiento en masa) permite aunar esfuerzos, pero también impone sus propios desafíos (por ejemplo, el desarrollo de herramientas y procedimientos para la gestión y el análisis de grandes cantidades de datos).

Algunos resultados: análisis de la aplicación

El análisis de las propuestas didácticas se realiza a través de los aspectos variacionales, los cuales permitieron formar un engranaje entre estudiante, práctica de modelación, ambiente y profesor para llegar a la consecución de los objetivos propuestos en este trabajo de investigación. Para este análisis se toman como referencia algunos resultados de las dos secuencias dadas propuestos por los estudiantes.

El tiempo como variable independiente

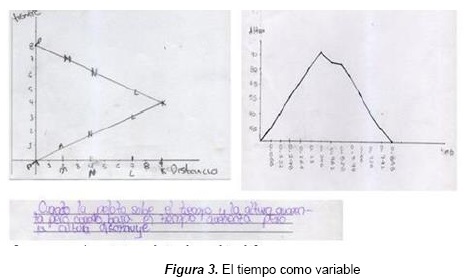
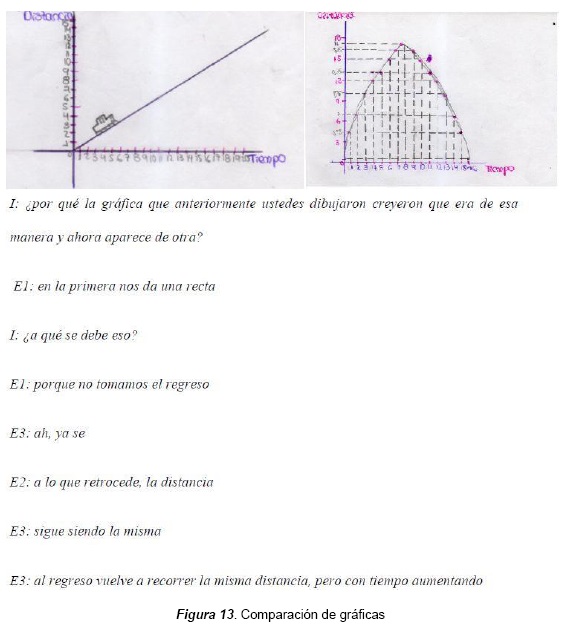
A través de la modelación se quiere relacionar el conocimiento científico (trayectoria que realiza un fenómeno determinado) con el conocimiento escolar (el tiempo como variable independiente, lo que se aprende institucionalmente). Se estableció que la mayoría de los estudiantes reconocen que el tiempo es una magnitud que siempre es positiva y no tiene regreso, siempre va aumentado, como se muestra en las dos gráficas de la figura 3, que corresponden, respectivamente, a las preguntas 2 y 6 de la secuencia 2. En la respuesta de la pregunta 5 de esta misma secuencia, como se muestra en el escrito dado por el estudiante en la figura 3, toman el tiempo como algo progresivo mientras la otra variable puede aumentar o disminuir. Algunos al graficar no sitúan el tiempo en el eje horizontal, como se observa en la primera gráfica de la figura 3, pues no es relevante el establecer la variable el tiempo en el eje horizontal. Generalmente reconocen el tiempo como variable en todas las preguntas de las secuencias que hacían alusión al tiempo dándole un significado. Aunque es una convención situar el tiempo, variable independiente, en el eje horizontal, por ahora parece que se han puesto en juego significados más reales para el estudiante. A través del análisis del tiempo se puede establecer que los estudiantes con sus acciones reconocen un antes y un después. Lo anterior se observa en las dos gráficas, donde el estudiante determina un tiempo localizando un punto que establece la ida y el regreso o un subir o bajar.

En algunas ocasiones los estudiantes toman el tiempo como si fuera una distancia que puede aumentar y en otras regresar, como se manifiesta en el diálogo realizado por ellos que se muestra en la figura 4.

El estudiante utiliza la tabla numérica para reconocer que el tiempo siempre aumenta, mientras que otras variables pueden regresar. Esto lo plasma en la respuesta a la pregunta 6 de la secuencia (1), primer escrito de la figura 5, cuando se le pide que comente la relación de los datos numéricos del tiempo con referencia a la distancia. En este momento, el estudiante toma datos de tiempo del fenómeno del auto en movimiento y los compara con el valor de distancia respectivo y plasma su pensamiento en el escrito. Lo mismo argumenta el estudiante en la pregunta 5 de la secuencia (2), como lo manifiesta la afirmación "el tiempo siempre aumenta".

Uso de la gráfica: intervalos y puntos clave

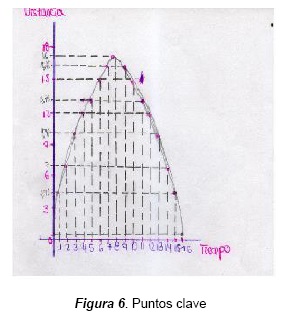
Para responder las preguntas propuestas, el estudiante identifica en la gráfica puntos clave o significativos, ya sea numérica o posicionalmente, utilizándolos para hallar las coordenadas de intersección. En la gráfica de la figura 6, tomada de la pregunta 7 de la secuencia 1, se puede ver cómo los puntos clave le dan forma a la gráfica y además marcan lugares que indican inflexiones. Las parejas ordenadas tiempo-distancia las toman de las tablas elaboradas por cada estudiante: las distancias están marcadas y el contador del applet mide el tiempo.

El estudiante desarrolla argumentos y herramientas que fortalecen el conocimiento sobre función cuadrática cuando compara intervalos, como se observa en el escrito de la figura 7, referente a la pregunta 2 de la secuencia (1), cuando se les pide comparar tramos del movimiento. Puede verse que toman dos tramos del movimiento y los comparan en forma numérica. Se evidencia que reconocen que para tramos de distancias iguales existen tiempos diferentes, lo cual da bases para pensar que los intervalos ayudan a establecer un modelo gráfico.

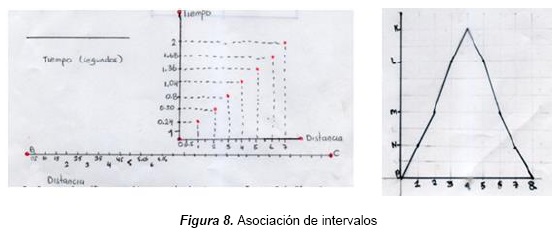
El estudiante establece intervalos, como en el caso del tiempo con otra variable, ya sea distancia o altura, determinando parejas como se observa en las gráficas de la figura (8), donde toma el tiempo y lo une con el valor correspondiente de distancia. Podemos constatar en la primera gráfica de la figura obtenida de la secuencia (1), pregunta 4, que el estudiante reconoce los cambios que sufren las variables de los objetos en movimiento, ya sean cualitativos o cuantitativos, llevando intervalos y puntos de forma unidimensional a bidimensional. En la segunda gráfica correspondiente a la secuencia (2), pregunta 2, el estudiante toma los valores de tiempo al pasar la pelota por los puntos marcados que se encuentran a determinada altura y los traslada a una gráfica, estableciendo puntos bidimensionales en forma numérica y posicional en el gráfico cartesiano, donde se le da significado a un punto tanto por sus coordenadas numéricas como por su posición en el plano. De esta manera el estudiante traslada o extrae puntos del movimiento de la pelota y los localiza en una gráfica cartesiana, para indicar el arriba, el abajo, el más arriba o el más abajo. Las dos gráficas dan cuenta del uso de las gráficas por parte del estudiante trasladando intervalos unidimensionales a dos dimensiones; es un argumento que se desarrolla para resignificar intervalos usando la gráfica. Aquí se hace evidente cómo la práctica de modelación favorece dicho desarrollo y la resignificación correspondiente.

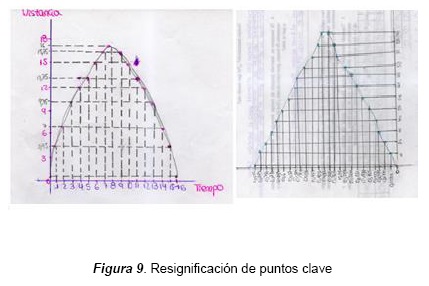
El estudiante usa la gráfica resignificando puntos clave cuando en la figura 9 establece puntos bidimensionales (altura, tiempo) en un plano cartesiano. Podemos ver que las líneas punteadas o continuas asocian cada punto con un valor en el tiempo (eje X) y uno en la distancia (eje Y). En esta doble asociación está trabajando con puntos coordenados. En la primera gráfica de la figura 9 podemos ver que los valores de la variable dependiente no están dados en forma proporcional ni secuencial, pero el tiempo sí. En la segunda gráfica de la figura 9 vemos que el estudiante pareciera estar trabajando en lo que institucionalmente se conoce como el segundo cuadrante. Sin embargo, no es así porque los valores del eje X no son negativos; entonces podemos decir que el estudiante indiferentemente toma para graficar cualquier cuadrante, mostrando que su único interés es realizar la gráfica. La primera gráfica está tomada de la secuencia (1), pregunta 7, y la segunda de la secuencia (2), pregunta 6.

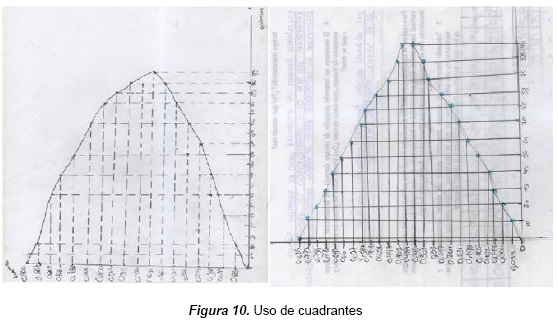
En la gráfica de la figura 10, extraída de la secuencia (2) pregunta 7, se observa nuevamente que el uso de los cuadrantes para el estudiante es algo intrascendental y por eso realiza la gráfica en el llamado segundo cuadrante, de acuerdo a las convenciones establecidas institucionalmente o por el discurso escolar del profesor. Las gráficas desarrolladas por los estudiantes muestran que se conservan los valores del eje (X) positivos, de la manera como los obtuvo de la observación del fenómeno sin interesar que la progresión va hacia la izquierda. Parece ser que ante esta situación el estudiante resignifica intervalos y puntos clave de acuerdo al posicionamiento de las parejas ordenadas sin interesar el cuadrante.

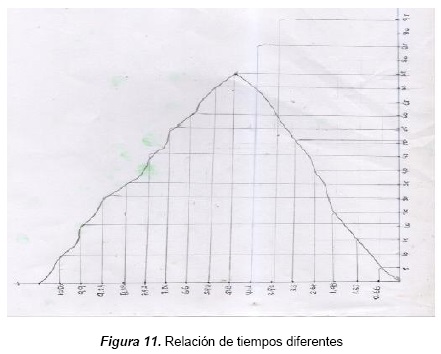
El estudiante reconoce que para valores de tiempo diferentes se repiten valores de distancia o altura, como se observa en la figura 11, correspondiente a la secuencia (1), pregunta 7. Allí crea una relación entre dos variables, en este caso tiempo y distancia; así muestra que para un mismo valor de distancia existen tiempos diferentes. Esto permite inferir que los intervalos junto a los puntos clave son importantes para romper con la creencia de que todo fenómeno se debe graficar en forma lineal.

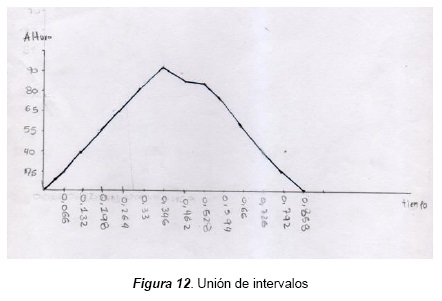
El estudiante establece un tiempo medio, en el cual sucede el regreso del objeto y, usándolo como referencia, puede obtener intervalos de distancia o altura. Al hacerlo, el estudiante reconoce que no todas las variables de los fenómenos se representan como modelos lineales, según se observa en la gráfica de la figura 12, tomada de la secuencia (2) pregunta 6, al evidenciar que uniendo intervalos se forma una curva.

El estudiante cuando compara las gráficas reconoce que los puntos clave lo ayudan a romper con la linealidad en los fenómenos que se presentan, y que no todos los fenómenos tienen comportamiento lineal. Esto se puede observar en las gráficas de la figura 13, donde el estudiante compara las gráficas y se da cuenta de que en la primera no toma el movimiento de regreso. En la segunda, la posición de los puntos le da la forma de la gráfica cartesiana del fenómeno de movimiento. En el diálogo presentado en la figura 13 se plasma la respuesta de por qué las gráficas realizadas por ellos antes y después de la toma de datos son diferentes. La primera hace referencia a la secuencia (1), pregunta 4, y la segunda corresponde a la pregunta 7 de la misma secuencia.

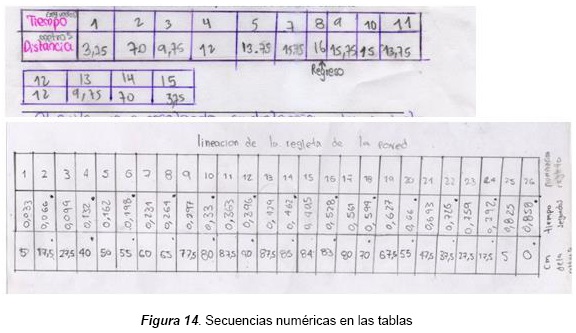
Las tablas sirven de organizador de los datos numéricos para llevarlos a la gráfica; pero también dan indicios del tipo de proporcionalidad que puede existir entre las variables participantes, tiempo y distancia o altura, así como del comportamiento curvo del fenómeno. En la figura 14, a partir de un valor establecido de tiempo se determina un valor para la distancia o la altura. Estas son un punto de unión entre el fenómeno real y el esbozo de una gráfica, porque los datos de las variables se organizan en tablas que facilitan el dibujo de la gráfica. El uso de secuencias numéricas permitió a los estudiantes ordenar los datos y observar su relevancia en la graficación, así pudieron establecer una relación de fenómeno-sucesiones numéricas y sucesiones numéricas-gráfica. Las tablas son un punto de unión entre el fenómeno real y el esbozo de una gráfica porque, de acuerdo al desarrollo de la actividad, el estudiante toma directamente los datos recopilados en las tablas para realizar el esbozo de las gráficas cartesianas. Las tablas les permiten ordenar datos y observar su relevancia en la graficación, así como establecer una relación sucesiones numéricas-gráfica y fenómeno-sucesiones numéricas.

Podemos determinar que el estudiante resignifica la función cuadrática por medio del aspecto variacional de las secuencias numéricas en la tabla cuando establece intervalos iguales o desiguales de tiempo y determina su respectiva pareja, cuando es capaz de generar unos datos y graficarlos, cuando en la misma tabla puede establecer relaciones tiempo-distancia o tiempo-altura y las dos tablas manifiestan estas relaciones. En la primera tabla establece valores de tiempo secuenciados y para cada uno de ellos halla el valor correspondiente de la otra variable; esta tabla corresponde al movimiento del auto en la secuencia (1), pregunta 6. En la segunda tabla, correspondiente a la secuencia (2), pregunta 5, establece la proporción entre sus datos mientras que en la primera establece puntos de inflexión como el punto bidimensional (altura, tiempo) donde sucede el regreso. En las dos secuencias propuestas de ida y regreso del auto y lanzamiento de una pelota, el estudiante expresa a través de las tablas las relaciones numéricas obtenidas a partir de la observación del fenómeno.

Comentarios finales

Las secuencias diseñadas fueron ideadas con el fin de discutir los aspectos variacionales de la función cuadrática favorecidos intencionalmente por la práctica de modelación como parte activa en el proceso enseñanza-aprendizaje de la función cuadrática. La investigación ha contribuido a formar un marco de referencia que involucra la modelación, los aspectos variacionales, el uso de gráficas, los experimentos de diseño y el uso de la tecnología como herramienta.

La investigación nos lleva a generar una base de significados alrededor de elementos variacionales para la significación de la función cuadrática en un contexto socioepistemológico. La aplicación de secuencias es realizable en el aula de clase para estudiantes entre 12-13 años que hasta ahora comienzan el trasegar en el precálculo.

En las investigaciones en las que la modelación se toma como una práctica es factible que se resignifique conocimiento matemático usando los experimentos de diseño como complemento, de forma que no solo es valioso lo que el estudiante plasma en un escrito, sino que además sus relaciones con el medio y con sus semejantes, sus formas de expresar y de proponer brindarán respuestas a algunos interrogantes de la investigación no observables en el

discurso escolar cotidiano. Esto nos lleva a creer que este trabajo puede ser un referente para el proceso de enseñanza-aprendizaje de la matemática a nivel de bachillerato y con adaptaciones a otros niveles. Además podemos creer que estableciendo una relación acorde entre la modelación y los experimentos de diseño, se posibilita de una manera más activa la resignificación de conocimiento, en nuestro caso el de función cuadrática.

Cuando los estudiantes compararon las gráficas que realizaron en grupo, inicialmente como bosquejo y luego con los datos de la tabla, se admiraron de ver el comportamiento de la gráfica en forma de curva. Algunos comentaron que al establecer parejas ordenadas se observa como si fueran escaleras que le dan forma a la gráfica. Esto manifiesta que los estudiantes reconocen que no todo fenómeno se representa en forma de línea recta en una gráfica, lo que rompe con la linealidad en los fenómenos. Se puede comentar que las gráficas en el caso que nos compete son básicas para observar las variaciones de las magnitudes establecidas, determinar el comportamiento del fenómeno, establecer relaciones distancia-tiempo o altura-tiempo, establecer proporcionalidad, establecer puntos clave, establecer parejas ordenadas y reconocer intervalos (algo que se puede partir en porciones).

En la investigación es relevante que se tome el tiempo como variable independiente, debido a que en la escuela está institucionalizado de este modo y el objetivo del trabajo es significarlo. A través de la modelación se quiere relacionar el conocimiento científico (trayectorias visibles a la imaginación) con el conocimiento escolar (el tiempo como variable independiente). El estudiante en algunos casos toma el tiempo como una distancia, en otras lo toma en el eje vertical; es recomendable reconocer y realizar más investigación al respecto, los significados que podrían generarse al tomar el tiempo, no como variable independiente -según lo establece el currículo- sino como una variable cualquiera.

El uso de gráficas en intervalos y puntos clave permitió a los estudiantes reconocer que los puntos clave ayudan a que se rompa con la linealidad en los fenómenos que se presentan, y que no todos los fenómenos tienen comportamiento lineal. Los puntos clave les permiten visualizar cambios y, con estos, representar el comportamiento curvo del fenómeno. Los intervalos en las gráficas no solamente los usan para unir puntos, sino además para correlacionar el tiempo con la distancia o la altura a través de la cuadrícula, para establecer parejas ordenadas y también les ayudan a identificar los cambios que sufren los objetos en movimiento ya sean cualitativos o cuantitativos.

El uso de las tablas con secuencias numéricas establece relaciones y proporcionalidad entre las variables participantes. El uso de secuencias numéricas les permitió a los estudiantes ordenar los datos y observar su relevancia en la graficación, donde aprecian el comportamiento curvo de algunos fenómenos, como el de la investigación. La toma de datos directamente del fenómeno permitió que el estudiante relacionara el fenómeno con las secuencias numéricas; de esta manera pudo llevarlas a una gráfica e integrar los dos componentes: secuencias numéricas y uso de gráficas.

El tener como referente los experimentos de diseño permitió reconocer las posturas de los estudiantes en las secuencias expuestas. Esto, con la ayuda de los gestos, los movimientos, las acciones, las intervenciones y las proposiciones que realizaron los estudiantes, captadas en videos y audios, es el complemento necesario que se tuvo en cuenta en el análisis de resultados.

Referencias bibliográficas

Arrieta, J. (2003). Las prácticas de modelación como proceso de matematización en el aula (tesis inédita de doctorado). DME, Cinvestav-IPN, México.

Briceño, O. (2014). Una secuencia de modelación para la introducción significativa de la función cuadrática (tesis inédita de maestría). Cicata: México.

Buendía, G. (2012). El uso de las gráficas cartesianas. Un estudio con profesores. Red de Revistas Científicas de América Latina, el Caribe, España y Portugal, 24(2), 9-35.

Buendía, G. & Montiel, G. (2011). Propuesta metodológica para la investigación socioepistemológica. Memorias de la XIV escuela de invierno en matemática educativa (pp. 443-454). México.

Cobb, P.; Confrey, J.; diSessa, A.; Lehrer, R. & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.

Confrey, J. (2006). The evolution of design studies as methodology. En R. K. Sawyer (ed.). The Cambridge Handbook of the Learning Sciences (pp. 135-152). Nueva York: Cambridge University Press.

Cordero, F. & Suárez, L. (2005). Modelación de matemática educativa. Acta Latinoamericana de Matemática Educativa, 18, 639-644.

Córdoba, F. (2011). La modelación en Matemática Educativa: una práctica para el trabajo de aula en ingeniería (tesis inédita de maestría). Cicata-IPN, México.

Díaz, L. (2005). Profundizando en los entendimientos estudiantiles de variación. Revista Latinoamericana de Investigación en Matemática educativa, 8(2), 145-168.

Dolores, C.; Alarcón, G. & Albarrán, D. (2002). Concepciones alternativas sobre las gráficas cartesianas del movimiento: el caso de la velocidad y la trayectoria. Revista Latinoamericana de Investigación en Matemática Educativa, Relime, 5(3), 225-250.

Mercado, L.; Aguas, N. & Arrieta, W. (2010). Comprensión del concepto de función a través de situaciones problema relacionadas con el contexto. En P. Lestón (ed.). Acta Latinoamericana de Matemática Educativa 23, 495-503.

Pech, V. & Ordaz, M. (2010). Las producciones de los estudiantes sobre el concepto función en situaciones variacionales. En P. Lestón (ed.), Acta Latinoamericana de Matemática Educativa 23, 15-22.

Villa, J. (2008). El concepto de función. Una mirada desde las matemáticas escolares. En C. Crespo, C. Oropeza y H. Parra (eds). Acta Latinoamericana de Educación Matemática, 21, 245-254

Forma de citar este artículo

Briceño, O. y Buendía, G. (2014). Una secuencia para la introducción de la función cuadrática a través de la resignificación de aspectos variacionales. Tecné, Epistemey Didaxis: TED, No. 39; p.__-__.