Diferencias trascendentales entre matematización de la física y matematización para la enseñanza de la física

Diferencias trascendentales entre matematización de la física y matematización para la enseñanza de la física

Transcendental Differences Between the Mathematization of Physics and Mathematisation for Teaching Physics

Diferenças transcendentais entre a Matematização da física e a matematização para o ensino da física

Diego Fabián Vizcaino Arévalo^*
Eduardo Adolfo Terrazzan^**

^* Doctor en Educación en Ciencias. UNESP (Brasil). Correo electrónico: d_vizcaino@yahoo.com
^** Doctor investigador CNPQ (Brasil). Docente Universidad Federal de Santa María, Brasil. Correo electrónico: eduterrabr@yahoo.com.br

Para citar este artículo:
Vizcaino Arévalo, D. F., Terrazzan, E. A. (2015) Diferencias trascendentales entre matematización de la física y matematización para la enseñanza de la física. Revista de la Facultad de Ciencia y Tecnología -Tecné, Episteme y Didaxis, (38), 95-111.

Artículo recibido el 09-08-2015 y aprobado el 25-10-2015

Resumen

La comprensión y formalización de las leyes de la física ha sido posible gracias a la combinación de diferentes tipos de aportes, dentro de los cuales la matematización de la física ha desempeñado un papel importante, permitiéndole a la física presentar avances importantes en términos de nuevos descubrimientos y en la formalización de teorías altamente predictivas. Esto ha llevado a pensar que utilizar las formas matemáticas adoptadas por la física como parte de su estructura de explicación, justifiquen la enseñanza de la física basada en la matematización. Por tal razón, se hace necesario entender el significado de la matematización no solo en la física, sino también en su enseñanza, reconociendo sus alcances y restricciones. En este trabajo se presenta un estudio acerca de la relación de la explicación y el lenguaje en la matematización de la física, verificando su existencia en tres momentos históricos de la física y comparando con lo obtenido en la literatura acerca del significado de matematización atribuido en la enseñanza de la física. Se encontró que son diferentes las concepciones de matematización para la física y matematización para la enseñanza de la física, y se mencionan algunas de sus implicaciones en el ámbito educativo.

Palabras clave: Didáctica de las ciencias, enseñanza de la física, matematización, explicación, lenguaje, historia de la física.

Abstract

Understanding and formalizing the laws of physics has been made possible by the combination of different types of contributions, within which the mathematization of physics has played an important role, allowing the physical present significant progress in terms of new discoveries and formalizing highly predictive theories. This has led to the suggestion that use mathematical forms taken by physics as part of its structure of explanation, justify the teaching of physics based on mathematisation. For this reason, it is necessary to clearly understand the meaning of the mathematization not only in physics but also in the teaching of physics, recognizing its scope and restrictions. We present a study about the relationship of explanation and language in mathematization of physics, verifying their existence in three historical moments of physical and compared with those obtained in the literature about the meaning attributed to mathematisation of physics in teaching. We found that they are different conceptions of mathematization for physical and mathematisation for teaching physics and mentioned some of its implications in education.

Keywords: Science education; Physics education; mathematisation; explanation; language; physics education; history of physics.

Resumo

Compreender e formalizar as leis da física tem sido possível pela combinação de diferentes tipos de contribuições, no âmbito do qual a matematização da física tem desempenhado um papel importante, permitindo à física apresentar progressos significativos em termos de novas descobertas e formalização de teorias altamente preditivas. Isto levou a pensar que as formas da Matemática tomadas pela física como parte de sua estrutura de explicação, justificam o ensino da física baseado em matematização. Por esta razão, é necessário entender claramente o significado da matematização não só na física, mas também no ensino da Física, reconhecendo o seu âmbito e restrições. Nós apresentamos um estudo sobre a relação de explicação e linguagem na matematização da física, onde foi verificada sua existência em três momentos históricos da física e comparados com os obtidos na literatura do significado atribuído à matematização no ensino da física. Descobrimos diferenças de concepções entre Matematização para física e matematização para o ensino de física e fazemos uma reflexão de algumas de suas implicações na educação.

Palavras-chave: Didatica das Ciencias; Ensino de Física; Matematização, explicação; linguagem; historia da física.

Introducción

En las concepciones sobre matematización aparecen tres aspectos interrelacionados en los estudios sobre la evolución de la física: el primero se refiere a las diferentes consideraciones sobre qué es explicar un fenómeno físico, que a su vez depende del lenguaje apropiado para presentar tales explicaciones y que, en últimas, se relaciona con lo que se considera matematizar un fenómeno físico.

Para matizar cómo estos aspectos han influido en el desarrollo de la física, tratamos la relación física-matemáticas en tres momentos históricos del desarrollo de la física, según la clasificación propuesta por autores como Paty (2003), Gingras (2001) y Cantor (1977), en donde la primera época trata sobre la filosofía natural desarrollada en la Grecia antigua; la segunda sobre la revolución científica a partir del siglo XV, y la tercera, desde los comienzos del siglo XX con el surgimiento de la física moderna y su desarrollo.

Reflexiones sobre "explicación", "lenguaje" y "matematización" en la historia de la física

Hablar sobre qué es explicar implica pensar en ¿explicar qué para quién? Hechos que para algunos científicos están explicados pueden ser un completo misterio para los no científicos; o pueden no estar claros para otros científicos de la misma época. También, fenómenos que se consideran explicados en alguna época, pueden ser explicados desde lógicas diferentes en otras épocas.

Para Hanson (1985), la explicación parte de un efecto sicológico. Explicar algún x sorprendente consiste en descomponer x en elementos menores, cada uno de ellos referidos a una situación previa carente de sorpresa o novedad de cualquier tipo (p. 36). También afirma que una explicación científica, por lo general, se presenta asociada la una ley conocida que puede desencadenar una serie de sucesos de tipo causal.

La explicación en el ámbito científico se relaciona con la mayor comprensión del porqué ocurren determinados fenómenos. Para Galileo, tal capacidad de descripción de los fenómenos se encuentra en la matemática. Según él y sus contemporáneos, la matemática ofrece la técnica para ordenar y comprender la naturaleza. Así, en el estudio del fenómeno de la gravedad durante los siglos XVII y XVIII, la explicación significaba describir el mecanismo físico envuelto en la caída de los cuerpos. En este contexto, la teoría newtoniana permitió pensar las realidades concretas a partir de proposiciones matemáticas abstractas, aun cuando tales descripciones no hablaran directamente del porqué ocurre el fenómeno.

Por tanto, la forma elíptica de las órbitas planetarias fueron explicadas basadas en la existencia de una fuerza centrípeta que disminuye con relación al inverso del cuadrado de la distancia; pero esto no explicaba la naturaleza de tal fuerza, lo que llevó a muchos filósofos a entender en esta proposición una demostración matemática y no una demostración física, pero que al final ofrece una nueva manera de explicar, combinando la experiencia sensorial con la formulación de cálculos.

El significado del termino explicación continuó evolucionando durante los siguientes siglos. La relación entre el mundo real, ontológico y el mundo abstracto fue exigiendo la idealización de los sistemas de forma que se pudiera generalizar resultados, pero siempre asociados al problema epistemológico de definir los fundamentos sobre los cuales son formuladas las leyes físicas.

Entre las propuestas acerca de explicación en el siglo XX, destacamos la de Hempel y Oppenheim (1948), y Carnap (1966/1973). Ellos proponen un modelo de explicación científica que debe ser dada en términos de leyes; no puede ser dada sin el uso de una ley. Junto con esto, para Hempel y Oppenheim la explicación científica debe responder tanto al qué como a los porqués de los fenómenos, pero siendo coherente con la ley científica, excluyendo agentes metafísicos en la explicación adecuada del fenómeno (Carnap, 1973, p. 20).

Para Holton y Brush (2001), las leyes de la física son generalmente relaciones matemáticas entre magnitudes expresadas por medio de funciones que determinan el tipo de relación entre las variables x, y, z, las cuales permiten un valor numérico dentro de una gama de valores, en función de las condiciones dadas al sistema observado. Los autores afirman:

The insistence on quantitative concepts must, of course, appear incomprehensible until we reorganize that the Work of the physical scientist is base on a faith as ancient as it is astonishing, namely, that nature Works according to mathematical laws and that the observations are explained when we find the mathematical law relating the observations (Holton y Brush, 2001, p. 165).

En este caso podemos decir que para estos autores la explicación está directamente asociada a descubrir las leyes matemáticas que describan los observables, basadas en la descripción causa-efecto entre las variables.

En el surgimiento de la física moderna este hecho fue de capital importancia dado que los fenómenos son descritos de forma cada vez más abstracta; se trata de fenómenos que no son tan cercanos a la experiencia sensorial inmediata ni son susceptibles de observación y medición directa. Para ser estudiados se necesita de métodos intermedios. Por ejemplo, el papel del científico que estudiaba la realidad física de la naturaleza en el siglo XVI era de ser intérprete de dicha realidad, mientras que en los siglos siguientes, el problema de la medición y de la observación ubicaba al científico como parte de la misma realidad que pretendía explicar.

De esta forma, explicar no es el simple hecho de describir con palabras las relaciones representadas en una ecuación; la explicación se dá necesariamente cuando hay comprensión de las representaciones del fenómeno, tanto en el campo de las funciones que relacionan las magnitudes involucradas, como en el campo de los porqués de la existencia de tales funciones.

Al discutir sobre lo que es explicar, surge la pregunta por el lenguaje con el cual es posible dar una explicación. De acuerdo con Carnap (1973, p. 107), el método cuantitativo, utilizado por primera vez de forma precisa por Galileo, introdujo reglas explícitas que le permitían tener un vocabulario más eficiente, aún sabiendo que antes de la introducción de un concepto había docenas de adjetivos cualitativos para describir los estados posibles de un objeto con respecto a una magnitud. Por ejemplo, sin el concepto de temperatura tendríamos que hablar de cosas que están muy calientes, calientes, cálidas, tibias, frescas, frías, etc. Por tanto, la principal ventaja del lenguaje, en términos cuantitativos, es que permite expresar conceptos que a su vez facilitan la formulación de leyes cuantitativas las cuales, a su vez, posibilitan la explicación de los fenómenos y la predicción de otros nuevos. Desde esta perspectiva, según Carnap, la palabra lenguaje, en física, debe ser utilizada en un sentido extraordinariamente amplio, referido a todo procedimiento que objetive comunicar información sobre el mundo exterior: palabras, cuadros, dibujos, imágenes, diagramas, ecuaciones, etc. (Carnap, 1973, p. 144).

A su vez, el lenguaje de la física fue transformándose en representaciones cada vez más abstractas en función de las necesidades de describir de forma apropiada los problemas estudiados en los diferentes momentos históricos. Para la época de Arquímedes no era necesario asociar sentido físico a una expresión matemática, dado que la demostración por medio de métodos matemáticos era suficiente para ser considerado como verdad. Durante los siglos XVI y XVIII, la relación entre física y matemática estaba mediada por la experimentación y la descripción precisa del comportamiento de los sistemas; por consiguiente, el lenguaje debía dar cuenta de esta precisión y a su vez debía permitir predecir los comportamientos de los sistemas. Con el surgimiento de la física moderna, el sentido físico de las representaciones matemáticas ganó más importancia, ya que los sistemas físicos estudiados no obedecían a características de lo cotidiano, generando la necesidad de crear un nuevo lenguaje para describir, basados por ejemplo en geometrías no euclidianas, nuevos operadores o nuevas funciones.

Esta nueva realidad nos lleva a interesarnos por la matematización del lenguaje de la física. De acuerdo con el epistemólogo Paty (2005), la matematización se justifica por la necesidad de expresar las propiedades de los conceptos y de las variables, y se constituyen en un principio de explicación. Paty muestra cómo a través de los últimos tres siglos, las matematizaciones han ofrecido credibilidad en las teorías, en la medida en que ha sido posible formular, de forma exacta, la especifidad de los fenómenos físicos. Él compara la inteligibilidad cartesiana, que entiende acciones producidas por choques, con la inteligibilidad newtoniana, que entiende acciones por atracción, de forma que el estatuto de tal atracción se fue transformando en un principio de explicación para la teoría del sistema solar, y por último la inteligibilidad de la relatividad de Einstein que tiene nuevos niveles de racionalización con conceptos más simples y homogéneos (Paty, 2005, p. 380).

En términos generales, la matematización de la física es definida como un proceso mediante el cual las metodologías de trabajo de los físicos se fueron interrelacionando cada vez más con los símbolos, conceptos y metodologías de trabajo de la matemática, para constituir explicaciones más complejas.

La relación entre física y matemática expresada en tres momentos históricos de la física

La relación entre física y matemática, en la época de Arquímedes, estaba mediada por las posibilidades de considerar como verdaderos los principios de la mecánica solamente a partir de las demostraciones de la geometría, sin tener en cuenta la experimentación como parte del proceso de búsqueda de la verdad, ya que el hecho de estudiar los fenómenos de la naturaleza por medio de técnicas experimentales era considerado un obstáculo en la comprensión de lo esencial de la naturaleza.

La ontología era de dominio exclusivo de la física o filosofía de la naturaleza, cuyo lenguaje era ambiguo ya que sus descripciones eran elaboradas con características cualitativas. Según Bochner (1991), Aristóteles describía la naturaleza por medio de procesos utilizando conceptos ambiguos como el de kinesis para referirse al movimiento, dando una noción del concepto de energía. Pero al analizar este término aristotélico de energía, a partir de nuevas perspectivas, notamos que se presentan dificultades para distinguir entre los conceptos de fuerza, energía y momento.

De acuerdo con Holton y Brush (2001, p. 237), entre los siglos XVI y XVIII, se crearon algunos criterios básicos para entender un concepto como verdadero, por ejemplo: la posibilidad de ser definido sin contradicciones internas ni ambigüedades, en términos de observables y efectos medibles, identificando si las mediciones son de forma directa, o no, y probando su validez en una amplia variedad de descripciones y leyes, tanto conocidas como deducidas recientemente.

Se resalta la diferencia entre la concepción sobre la relación física-matemática en la época antigua —en la cual los fenómenos de la naturaleza eran estudiados a partir de la filosofía y demostrados desde la geometría—, y la perspectiva actual —cuando el estudio de los fenómenos físicos implica la definición de nuevos conceptos, creados teniendo en cuenta la observación metódica de sistemas, que a su vez son idealizados a fin de obtener la mayor cantidad de generalizaciones y aplicaciones posibles—. En este momento histórico, la descripción de los sistemas físicos se hace principalmente con base en relaciones entre símbolos que representan variables del sistema, construyendo expresiones que contienen principios lógicos, no solo de la geometría sino también del álgebra y del cálculo.

Bochner afirma: "La Física Teórica como tal, emancipada de la Mecánica Racional, realmente comenzó a existir con el concepto de energía" (Bochner, 1991, p.194). La medición de la energía generó la necesidad de utilizar conceptos de la matemática para representarla adecuadamente. Así, para describir los sistemas físicos fueron considerados los números reales, la idea de función y el desarrollo del álgebra abstracta, propuestos en la matemática durante el siglo XIX. Este hecho además fomentó discusiones sobre la comprensión de la relación entre física y matemática entre los filósofos de la ciencia.

A comienzos del siglo XX, surgieron grandes cuestionamientos sobre cómo entender los procesos de construcción de la ciencia, generando una serie de discusiones sobre el problema de la medición y la observación de los sistemas físicos, así como de la naturaleza de la causalidad, que tiene, como antecedentes, cuestionamientos sobre la relación entre física y matemática y de lo que significa entender la matemática como un lenguaje de la física. Con la física moderna surgieron también filósofos de las ciencias que ya no buscaban simplemente describir, o listar y comparar diversas formas de pensamiento, sino que pretendían mejorar el conocimiento de los procesos de construcción de la ciencia.

Un ejemplo que podemos referir en esta época es la propuesta de la ecuación de onda relativista, de Dirac, que causó gran impacto, pues su solución le permitió predecir la existencia de electrones con carga positiva llamados antielectrones, y en consecuencia predecir que para toda partícula elemental debía existir su correspondiente antipartícula.

Para la formulación de esta ley, Dirac se fundamentó en el uso de operadores matemáticos que actúan en una función de onda. Tales operadores sustituyen observables de la mecánica clásica, que son experimentalmente medibles (energía, cantidad de movimiento, etc.), e involucran derivadas parciales de primer orden, apropiadas para describir el caso de cantidades pequeñas de orden microscópico. Igualmente, Dirac utilizó operadores definidos en la mecánica cuántica, como el de la energía (E), y los de las componentes rectangulares (x, y, z) del momento lineal (p).

Uno de los grandes desafíos que orientó la forma de proceder de Dirac fue la búsqueda del sentido físico de la ecuación que obtuvo, cuya solución tenía una parte positiva y otra negativa, en la cual el signo negativo podía ser interpretado como el electrón que posee carga eléctrica negativa y el signo positivo como el antielectrón, con carga eléctrica positiva.

El problema de la interpretación física de las ecuaciones aparece con la mecánica cuántica, marcando una necesidad mayor de entender la relación entre física y matemática. Esta, para Dirac, se basa en una concepción de uso de los procesos matemáticos como principios orientadores para la comprensión de los fenómenos naturales, más que en la comprobación experimental. Según Kragh (1990), la filosofía de Dirac se caracteriza por su idea de belleza matemática, que nunca definió, pero que puede ser entendida como la conformación de las teorías de la física la partir de principios de simplicidad en la base matemática. Este autor argumentó que si aparecía una diferencia entre la teoría matemática y un resultado experimental y se necesitaba una nueva teoría matemática, esta debía ser más bella.

[...] If a discrepancy should turn up between the predictions of such a theory and an experimental result, one's first reaction would be to suspect experimental error, and only after exhaustive experimental checks would one accept the view that the theory needs modification, which would mean that one must look for a theory with a still more beautiful mathematical basis. (Dirac, citado por Kragh, 1990, p. 286)¹.

Uno de los problemas que afrontaban los físicos y filósofos de la física moderna era entender el papel del observador en el estudio de los sistemas físicos y preguntarse sobre lo que podría ser considerado como observable o no observable, y cómo caracterizar lo observado, en especial cuando se trata de estudiar sistemas microscópicos que se encuentran fuera de la experiencia sensorial del observador.

Para Dirac podían existir observables no medibles, siendo esta lógica una de las razones que, según Kragh (1990), le permitió formular la ecuación de onda asociada al electrón obedeciendo el postulado de simetría relativista, que dice que los cuatro componentes (espacio-temporales) de la función deben obedecer a cuatro ecuaciones de primer orden. Este carácter relativista de la ecuación de Dirac le ayudó a entender que el electrón poseía un estado de energía negativa, cuyo comportamiento resultaba paradójico, ya que, nunca un electrón había presentado la propiedad del signo de la carga eléctrica contrario. Pero el hecho de no poder verificar la existencia de tales partículas, no llevó a Dirac a desistir de su teoría, pues él consideraba que el desarrollo de la matemática utilizada para describir tal sistema poseía sentido físico y simplicidad, hecho que manifiesta una forma de entender la relación entre física y matemática como proceso físico-matemático.

El significado de matemática como lenguaje en el siglo XX

Henri Poincaré, en El valor de la ciencia (2000), publicado en 1905, resaltaba que la relación entre física y matemática va mas allá del mero uso de cálculos numéricos para el estudio de los fenómenos de la física, y otorga a la matemática un estatus de lenguaje que permite al físico explorar de mejor manera las leyes que vienen de la experiencia:

[...] el objetivo de la física matemática no es solamente facilitar al físico el cálculo numérico de ciertas constantes, [...] este es sobre todo el de facultar al físico el conocimiento de la armonía oculta de las cosas, haciendo con que las vea bajo una nueva perspectiva. (Poincaré, 2000, p. 94).

Propuestas más contemporáneas respecto al significado de matematización de la física se encuentran en los trabajos del epistemólogo Michel Paty, cuya temática se centra en el problema de la definición de las magnitudes. Él evidencia que científicos como Einstein se preocupaban por el carácter físico de los conceptos o de las variables, donde la matematización debía expresar las propiedades de tales magnitudes en sí mismas. Paty concluye:

[...] This inquiry into the original thought of magnitudes, and of physical magnitudes conceived through mathematization, leads us to suggest an extension of meaning for the concept of physical magnitude that puts emphasis on its relational and structural aspects rather than restraining it to a simple "numerically valued" acception. Such a broadening would have immediate implications on our comprehension of "non classical" aspects of contemporary physics in the quantum area and in dynamical systems. (Paty, 2003, p. 1).

El matemático Salomon Bochner, en El papel de la matemática en el desarrollo de la ciencia (1991), caracteriza la Matemática como un lenguaje de la ciencia, pero según él, un lenguaje en el sentido amplio de la palabra, como aquel medio que permite la comunicación. Esto significa que tal lenguaje se inscribe en los procesos de pensamiento con los cuales se crea y desarrolla la ciencia. Él dice: "[...] La matemática no es apenas para formular, clarificar y tornar manejables de forma rigurosa conceptos y leyes científicas [...] sino también, en ciertas situaciones cruciales se muestra como un elemento esencial tanto de su creación como de su desarrollo" (p. 237).

Estos cambios de tipo epistemológico en la historia de la física incidieron también en cambios de tipo ontológico. Objetos físicos que antiguamente se imaginaban como parte de la naturaleza como los flujos eléctricos o calóricos ya no se imaginan mas, y, objetos que antiguamente no se imaginaban como las antipartículas, hoy pueden ser descritos. Las posibilidades de introducir abstracción y generalización en las explicaciones, según Gingras (2001), han hecho que la concepción de la materia en términos de sustancias fuera desapareciendo y, en cambio, apareciera un énfasis en los aspectos relacionales de las teorías que explican la naturaleza de la materia. Podemos decir que a partir de una interpretación simplista de estas consecuencias, se ha creado en el imaginario colectivo la idea errada de que para entender la física moderna se necesita únicamente la manipulación de símbolos matemáticos sin una conexión entre los conceptos y los referentes intuitivos de los sujetos.

Estas ideas hablan de una relación necesaria y fundamental del uso de la matemática en la producción de la física, dejando ver que efectivamente es necesario comprender tal relación, considerando si la intensión es aprender física o investigar en física, ya que una cosa es pensar la matemática como un lenguaje que permite describir la naturaleza de forma apropiada, y otra muy diferente es la matemática como un lenguaje inscrito en los procesos de pensamiento, ya sea para organizar y expresar ideas, para interpretar hechos desde diversas perspectivas, o para comprender y explicar los fenómenos naturales.

En este punto surge la cuestión sobre las implicaciones de la comprensión de la física desde la relación física y matemática al pensar la enseñanza de la física. Como profesores de física se debe comprender cómo las relaciones entre física y matemática han sido desarrolladas en la construcción de conocimiento científico; y de otra parte, comprender los procesos de enseñanza/aprendizaje en el salón de clase. Estos se vuelven importantes aun cuando la física y la enseñanza de la física compartan el mismo saber disciplinar sobre el estudio de la naturaleza, son campos diferentes en su epistemología, fines, formas de evolución y soportes teóricos.

Significados de "matematización" en la enseñanza de la física

El estudio de la relación entre física y matemática en la evolución de la física no tiene el mismo carácter que el estudio de esta relación en la enseñanza de la física, así el segundo campo dependa en gran manera del primero. En otras palabras, comprender de qué manera el lenguaje de la física se fue matematizando durante su evolución, permite profundizar en el conocimiento de sus contenidos y, en consecuencia, puede garantizar una mayor preparación del profesor. Sin embargo, al llevar este conocimiento para el aula, el docente debe tomar en cuenta ciertas decisiones para orientar el aprendizaje por medio de procesos de matematización.

En la enseñanza de la física, tanto en educación media como en la universitaria, el sentido de términos como explicar, lenguaje y matematización se presentan de forma diferente a cómo se entiende cada uno de estos en la evolución de la física. El profesional de la educación, el profesor, no se dedica a buscar nuevas explicaciones de los fenómenos de la naturaleza como en la evolución de la física, pero dentro de su trabajo es una tarea explicar a otras personas él cómo se explica la naturaleza. Por tanto, el lenguaje como herramienta para describir y comunicar, debe moverse entre los lenguajes de la física (para explicar determinados fenómenos) y los de los alumnos ² (que necesitan comprender aspectos de la naturaleza), proceso que no se limita a la presentación de la matematización de la física a lo largo de la historia, sino que dentro de sus objetivos es importante orientar los alumnos a desarrollar sus propias matematizaciones.

Para corroborar esta hipótesis, se buscaron los usos del término matematización en algunas propuestas de la literatura, y que estudian la relación entre física y matemática en ámbitos educacionales.

Propuestas de usos de la matemática en la enseñanza de la física

El trabajo de Redish (2006) defiende la idea de que comprender la relación entre física y matemática implica distinguir entre lo que es hacer matemática y lo que es usar la matemática en el desarrollo de la física. Esto implica que el físico no aprende matemática y física de forma separada, para después juntar los dos conocimientos, pero toma el mundo físico describiendo sus conceptos por medio de representaciones matemáticas y así puede garantizar una interpretación física de tales representaciones para luego evaluar su validez en el mundo físico. Por tanto, no es en la matemática que se encuentra la validez de una expresión de la física, pero sí en la coherencia que dicha expresión presenta para describir la naturaleza.

Esta idea presentada por Redish, al transponerse para la enseñanza, puede ser interpretada de la siguiente manera: no tiene mucho sentido enseñar la matemática como prerrequisito para estudiar física, en espera de que tal prerrequisito garantice la comprensión de las descripciones formales de la física, ya que el aprendizaje de la matemática en sí mismo no garantiza aprender a usarla en otros contextos. Sin embargo, el aprendizaje de la física implica el aprendizaje de cómo usar símbolos y relaciones entre símbolos para poder expresar ideas y construir explicaciones.

Entonces, utilizar o asumir el carácter deductivo del formalismo matemático, en contextos de la enseñanza de la física, no significa enseñar a calcular valores por medio de una ecuación, sino llevar al alumno a comprender formas de relacionar magnitudes físicas, seleccionando apropiadamente determinadas estructuras matemáticas, a fin de comprender el uso y significado de las representaciones de los fenómenos físicos.

Bing y Redish (2009) defienden que resolver problemas de física en el aula implica desarrollar en el alumno habilidades complejas de raciocinio, llevándolo a la razón por la cual pueden o deben optar por el uso de determinados esquemas matemáticos y no otros en la solución de problemas de física.

Ellos observaron grupos de alumnos universitarios cuando trabajaban en grupo resolviendo problemas de física. Bing y Redish describían el pensamiento matemático de los estudiantes, y encontraron que los estudiantes se confunden al utilizar un conjunto limitado de habilidades o de raciocinios, sin percibir que un conjunto diferente de herramientas (que ya poseen y no sabe cómo utilizar) les podrían ayudar a resolver el problema de forma mas sencilla y rápida.

Los autores concluyen que la enseñanza de la física debe formar a los alumnos en un marco epistemológico (epistemological framing) que les permita interpretar el papel de la matemática en los desarrollos de la física. Por ejemplo, en torno de una expresión básica de la física como es , que relaciona la posición inicial X_I, la posición final X_f , la velocidad media 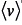y un intervalo de tiempo Δt, pueden ser estudiados diferentes papeles epistemológicos de esta expresión matemática en la comprensión de los fenómenos físicos. Papeles como:

1. La expresión en sí misma es un esquema de cálculo. Representa un esquema que permite calcular un resultado numérico con base en algunos datos conocidos; si el objeto en movimiento parte de una posición conocida, con un valor conocido de velocidad, se puede determinar la posición final para un tiempo determinado.

2. Representa una relación física entre las magnitudes. El significado de permite entender qué tan rápido el cuerpo se desplaza una unidad de tiempo y, conocida la posición inicial, permite completar la relación encontrando la posición final.

3. La representación matemática ofrece un sistema conciso de reglas que encierran resultados previamente construidos. La expresión matemática sintetiza leyes de la Física que se fueron consolidando históricamente.

4. La expresión interrelaciona una gran red de ideas matemáticas. Tal expresión,

- puede ser derivada por medio de la operación algebraica a partir de la definición de velocidad media,

- tiene la estructura conceptual de otras formas simbólicas ,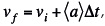

- puede ser interpretada a partir de un gráfico de velocidad,

- y puede ser vista como la solución de

Este trabajo y el de Tuminaro y Redish (2007) evidencian que los alumnos poseen un conjunto de estrategias para resolver problemas, que los autores llaman de juegos epistémicos (epistemic games), describiendo básicamente seis tipos de juegos: a) mapping meaning to mathematics, en el cual los alumnos comienzan comprendiendo conceptualmente la situación física descrita, para identificar el problema a resolver y en seguida avanzan en la solución cuantitativa; b) mapping mathematics to meaning, en el que los alumnos desarrollan una historia conceptual a partir de una ecuación física particular; c) physical mechanism game, aquí los alumnos construyen una historia del problema a partir de su sentido común de lo que es un mecanismo físico (ellos no se refieren a principios ni a ecuaciones); d) pictorial analysis game, en el cual los alumnos parten de una representación espacial relacionando los aspectos presentados en el problema para intentar deducir una solución; e) recursive plug-and-chug, en este caso los alumnos identifican cantidades y las unen mediante una ecuación, intentando obtener un resultado sin comprender lo que esto significa conceptualmente; f) transliteration to mathematics, donde los alumnos utilizan ejemplos trabajados para generar una solución sin el desarrollo de una compresión conceptual del ejemplo trabajado.

En la identificación y caracterización de estos seis tipos de juegos utilizados por los alumnos, los autores encontraron que, en la mayoría de las veces, los estudiantes ignoran o no tienen conciencia del papel de la matemática en la formulación de la física, una vez que una característica común es creer que pueden demostrar que aprendieron física cuando consiguen hallar la respuesta del problema. Aunque el profesor intente desmitificar porque es consciente de que la enseñanza de la física no debe ser enciclopédica ni basada exclusivamente en el uso de las ecuaciones para calcular valores, los alumnos no cambian su idea original, al percibir que lo que realmente los aprueba son las notas obtenidas en las evaluaciones, que generalmente exigen un alto grado de memorización y exigen que puedan aplicar ecuaciones y resolver problemas sin preocuparse por exponer la comprensión del fenómeno, ni por identificar ni manifestar que está utilizando un determinado esquema matemático.

En el problema identificado por estos autores podemos ver que el entendimiento de la matemática como lenguaje de la física, desde el punto de vista de los alumnos, está lejos de la concepción con la cual los científicos han construido la física a lo largo de su historia. La identificación de este tipo de problema justifica la necesidad de una investigación en enseñanza de la física que ofrezca resultados para aprender a modificar las concepciones ingenuas de los alumnos sobre la solución de problemas en el aprendizaje de la física. En este tópico, la literatura presenta en la actualidad una tendencia de propuestas de enseñanza en torno de la modelización como un proceso de formación de alumnos en habilidades apropiadas para la construcción y comprensión de modelos explicativos de los fenómenos físicos.

En la propuesta de enseñanza desde la modelización generalmente se asume que orientar los alumnos en actividades de modelaje facilita su formación en las habilidades necesarias para el dominio de las formas de representar los fenómenos físicos. Según Hestenes (1996), el uso del modelaje en la enseñanza de la física permite crear condiciones para aprender física de una forma más eficaz, entendiendo la física como una red compleja de modelos que se interrelacionan en un sistema de principios teóricos: "Models are units of structured knowledge used to represent observable patterns in physical phenomena. Accordingly, 'physical understanding' is a complex set of modeling skills, that is, cognitive skills for making and using models". (p. 7)³.

Tales unidades de estructuración del conocimiento son comúnmente entendidas en la enseñanza de la física como los problemas teóricos y su solución, que según el autor es un error, pues la solución de problemas es apenas una parte del proceso de modelaje. El método de enseñanza por modelización trata de orientar a los alumnos en la reestructuración de sus intuiciones envolviéndolos en construcciones explícitas y en la manipulación de representaciones estructuradas. Por tanto, es importante decidir qué enseñar y cómo enseñar.

La construcción del modelo involucra cuatro tipos de estructura: a) sistémica: partes internas del sistema, agentes externos ligados al sistema y conexiones entre las partes internas y externas; b) geométrica: posición con relación al sistema de referencia, relaciones geométricas entre las partes; c) temporal: cambios de las variables en función del tiempo, cambios por medio de ecuaciones diferenciales con leyes de interacción; d) de interacción: interacciones entre los nexos causales, generalmente en función de variables de estado.

En la enseñanza, el proceso de construcción del modelo puede ser elaborado siguiendo la descripción de las estructuras involucradas en el estudio del sistema físico para, posteriormente, comprender sus implicaciones y evaluar su validez; para esto se deben comparar las predicciones obtenidas de la estructura con los datos empíricos que representan el comportamiento del sistema (sabiendo que no se debe esperar una confirmación exacta de datos ya que todo modelo es una representación incompleta).

Desde esta perspectiva, Angell, Morten, Henriksen y Guttersrud (2008) consideran que la enseñanza de la física debe formar los alumnos entendiendo la naturaleza de la física como una empresa de modelaje, lo que significa formarlos para que, por medio del raciocinio, vinculen las representaciones experimentales con las conceptuales. Estos autores llaman a su propuesta abordaje empírico-matemático, para el cual proponen dos tipos de actividades: una que busca llevar el alumno a utilizar múltiples representaciones del fenómeno físico, y otra que busca enfatizar en que la producción de la física se basa en la construcción de modelos. Los tipos de representaciones son definidos en Guttersrud y Angell (2010) como: conceptuales, pictóricos, gráficos y matemáticos, entendiendo que, para que el alumno pueda transitar entre ellos necesita ser formado en habilidades de raciocinio con las cuales pueda categorizar, identificar, decidir, evaluar, concluir y comunicar.

A su vez, Uhden, Karam, Pietrocola y Pospiech (2012), y Karam (2012) comparten la misma perspectiva sobre ciclos de modelado con niveles gradativos de matematización en la formulación de las leyes físicas. Ellos resaltan que es necesario partir de la realidad del mundo para avanzar en la elaboración de modelos físico-matemáticos, no de forma lineal, un poco flexibles, hasta llegar a trabajar con cálculos de valores. Así, lo que ellos llaman matematización es la fase preliminar al trabajo con cálculos de valores, siendo esta etapa subdividida en varios momentos que van de las percepciones del mundo hasta las organizaciones de los esquemas que lo explican con su interpretación y validación de la realidad. Ellos afirman que en la fase de matematización, el científico practíca habilidades estructurantes del pensamiento, mientras que en la fase de cálculos el científico practíca habilidades técnicas.

Esto significa que al aplicar esta forma de entender la relación entre física y matemática por medio de la matematización en contextos de enseñanza, es necesario desarrollar en los alumnos un pensamiento físico-matemático, por medio de la comprensión de los conceptos de la física a partir de sus aspectos matemáticos, superando la dicotomía pensamiento cualitativo para la física y pensamiento cuantitativo para la matemática. Por tanto, el aprendizaje ocurre en la medida en que el alumno entiende el carácter deductivo del formalismo matemático, comprende las analogías que le permiten pensar fenómenos físicos desconocidos, desarrolla abstracciones, entre otras habilidades.

De esta manera, las habilidades técnicas están asociadas a saber hacer, mientras que las estructurantes están asociadas a saber por qué hacer, para qué y cuándo usar. De acuerdo con Karam y Pietrocola (2009) una de las habilidades estructurantes más importantes es la capacidad de identificar los aspectos que justifican la presencia de una estructura matemática en un modelo. Estos autores proponen un ejemplo de preguntas que se pueden hacer acerca de la estructura matemática de un problema físico:

- Por que as funciones trigonométricas (seno e co-seno) aparecem nas fórmulas matemáticas utilizadas na resolução destes três problemas? O que os mesmos têm em comum?

- Quais são os aspectos relevantes para que as funções trigonométricas sejam úteis como estruturas matemáticas para modelizar fenômenos físicos?

- Poderíamos trocar seno por co-seno (ou vice-versa) em cada um dos três problemas? Por quê? (Karam y Pietrocola, 2009, p. 197).

Este ejercicio lleva a comprender por qué ciertas estructuras matemáticas funcionan para explicar diversos problemas de la física y cuáles son las condiciones que deben cumplir tales situaciones para que puedan ser representadas con el mismo esquema matemático, además de entender las particularidades de cada situación.

En las propuestas de todos los autores mencionados no se considera eliminar los algoritmos en la enseñanza —ya que los conceptos y métodos de la física están profundamente influenciados por el pensamiento matemático—, pero sí asumen usarlos en un proceso que lleve el alumno a percibir una relación entre el formalismo matemático y la constitución de las teorías de la física, aun cuando estos autores presenten algunas diferencias en sus formas de entender la matematización en la enseñanza.

Este análisis se resalta cómo la matematización en procesos de enseñanza de la física tiene un sentido diferente de la matematización en la evolución de la física, ya que, en el primer caso la principal preocupación radica en la definición de procesos que orienten los alumnos; entre tanto, en el segundo caso, la preocupación se centra en la coherencia de las representaciones adecuadas para describir el mundo físico. De otro lado, es evidente la necesidad de continuar estudiando la relación física/matemática en la enseñanza de la física, buscando mayor comprensión del significado de la matematización en este campo y de sus posibilidades al ser llevada a la práctica educativa.

Reflexiones sobre "explicación, lenguaje y matematización en la enseñanza de la física"

De acuerdo con las posturas presentadas, se puede afirmar que explicar en la enseñanza de la física va más allá de relatar a los alumnos en qué consisten las leyes de la física. Este acto comienza con la planeación de actividades pensadas en orientar procesos de estudio de los fenómenos físicos, propiciando en el alumno una familiarización gradual con las formas de representar el comportamiento de los sistemas observados, para lo cual se hace necesario enseñarles a analizar la funcionalidad de las representaciones utilizadas.

Por tanto, explicar implica enseñar a organizar representaciones de los fenómenos, ya sea con imágenes espacio-temporales o no, pero también implica orientar para que los alumnos encuentren relaciones entre diversas imágenes, tanto como relaciones entre las imágenes y los símbolos, de forma que vayan construyendo un lenguaje por medio del cual puedan dar cuenta de la explicación de un fenómeno y, además, expresen pensamientos que no podrían haber tenido sin la constitución de este lenguaje. Esto implica que uno de los objetivos que debe cumplir el profesor al explicar en la enseñanza de la física, es llevar al alumno a explicar, lo cual le acarrea niveles de organización cognitivas mayores. Según Gómez-Moliné y Sanmartí, (2000): "El hecho de que un alumno (o profesor) se prepare para transmitir sus conocimientos, genera en su estructura cognitiva una mayor organización de la que generaría si intentara simplemente memorizarlos o repetirlos" (p. 272).

Por consiguiente, es necesario que el profesor diferencie entre resolver problemas tratando de fijar determinados conocimientos transmitidos con base en la formalización de las leyes de la Física, y resolver problemas con base en ejercicios o prácticas de esquematización y axiomatización en el estudio de los fenómenos físicos. Así, aun cuando un determinado modelo fundamenta una explicación científica, no se puede decir que ese modelo puesto en el salón de clase constituya en sí mismo una explicación para el alumno de la realidad física, esto quiere decir que la sola exposición de la representación de un fenómeno no explica el por qué de esa representación, así esta tenga sentido completo dentro de la ciencia. Significa afirmar que cómo una persona lleva a otra a comprender y conocer la ciencia no depende directamente de la ciencia por sí misma.

De este modo, es necesario orientar al alumno en la consolidación de un lenguaje cada vez más adecuado y eficiente para representar la realidad, sabiendo que tal representación está asociada a imágenes, símbolos y conceptos que conforman las leyes físicas, que tiene en cuenta las particularidades de la física; por ejemplo, que no siempre las leyes físicas tienen una realidad inmediata asociada y no siempre las imágenes responden a nociones espacio-temporales evidentes en nuestra realidad.

Es importante, además, diferenciar entre un lenguaje puramente matemático y un lenguaje matemático asociado a la representación de los fenómenos físicos, ya que en la matemática pura, el lenguaje tiene un carácter de abstracción diferente al de la física. Por ejemplo, no tiene el mismo significado una constante de la matemática como el número p, y una constante de la física como la constante de Planck (h), y no utiliza los símbolos de la misma forma para expresar cantidades o relaciones entre cantidades de la matemática, o para expresar ideas en la física.

La física necesita atribuir unidades de medida a los símbolos que representan cantidades y estas unidades de medida dependen de patrones o parámetros que pueden variar en función de los sistemas y condiciones consideradas, lo que no ocurre con los parámetros y las variables de la matemática. Por esta razón, es importante mostrar a los alumnos que las ecuaciones son más que fórmulas para calcular un valor numérico, ellas son relaciones entre símbolos que tienen significados específicos en función del sistema. De acuerdo con Redish y Gupta (2010),

Understanding an equation in physics is not limited to connecting the symbols to physical variables and being able to perform the operations in that equation. An important component is being able to connect the mathematical operations in the equation to their physical meaning and integrating the equation with its implications in the physical world. (p. 12)⁴

De estos autores es posible deducir que la matematización en la enseñanza de la física puede ser entendida como una estrategia de explicación, para lo cual es preciso formar al alumno en la construcción o reelaboración de un lenguaje específico, el cual va mas allá del dominio instrumental de las representaciones matemáticas del mundo físico, y se apoya en la comprensión del sentido de las representaciones.

Notas

¹ "Si una discrepancia surge entre las predicciones dadas por una teoría y los resultados experimentales, una primera reacción sería sospechar de algún error experimental y solamente después de verificar exhaustivamente el experimento es que uno acepta la visión de que es necesario modificar la teoría, es decir, buscar una teoría con una base matemática mucho más bonita" (traducción propia).
² En este trabajo, tomamos la definición de alumno según la Rae (rae 2015), y que es la persona que recibe enseñanza, respecto de un profesor o de la escuela, colegio o universidad donde estudia.
³ "Los modelos son unidades de conocimento estructurado usados para representar patrones observables en los fenómenos físicos. Así, 'la comprensión física' es un conjunto complejo de habilidades de modelage, es decir, habilidades cognitivas para producir y usar modelos" (traducción propia).
⁴ "La comprensión de una ecuación de la física no se limita a la conexión de los símbolos con las variables físicas y el domínio de las operaciones por medio de la ecuación. Una componente importante se refiere a la conexión de las operaciones matemáticas en la ecuación con sus significados físicos y, la relación entre la ecuación y sus implicaciones en el mundo físico" (traducción propia).

Referencias bibliográficas

Angell, C.; Morten, K.; Henriksen, E. y Guttersrud, Ø. (2008). An empirical-mathematical modelling approach to upper secondary physics. Physics Education 43(3), 256-264.

Bing, T.J. y Redish, E.F. (2009). Analyzing problem solving using math in physics: Epistemological framing via warrants. Physical Review Special Topics-Physics Education Research 5(2), 1-23.

Bochner, S. (1991). El papel de la matemática en el desarrollo de la ciencia. Madrid: Alianza Editorial.

Cantor, G.N. (1977). Berkeley, Reid, and the mathematization of mid-eighteenth-century optics. Journal of the History of Ideas 38(3), 429-448.

Carnap, R. (1973). Les fondements philosophiques de la physique. Trad. de Jean-Mathieu y Antonia Soulez. Paris: Librairie Armand Colin.

Gingras, Y. (2001). What did mathematics do to physics? History of science, 39, 383-416.

Gómez-Moliné, M. y Sanmartí, N. (2000). Reflexiones sobre el lenguaje de la ciencia y el aprendizaje. Educación Química 11(2). 266-273.

Guttersrud, Ø. y Angell, C. (2010). Mathematics in physics: Upper secondary physics students' competency to describe phenomena applying mathematical and graphical representations. En: girep-icpe mptl Conference. Reims France.

Hanson, N.R. (1985). Patrones de descubrimiento observación y explicación. Madrid: Alianza Editorial.

Hempel, C. y Oppenheim, P. (1948). Studies in the Logic of Explanation. Philosophy of Science 15(2), 135-175.

Hestenes, D. (1996). Modeling methodology for physics teachers. En: Proceedings of the International Conference on Undergraduate Physics Education. (pp. 935-958) College Park.

Holton, G. y Brush, S. (2001). Physics. The Human Adventure: from Copernicus to Einstein and Beyond. New Brunswick: Rutgers University Press.

Karam, R.A.S. (2012). Estruturação matemática do pensamento físico no ensino: uma ferramenta teórica para analisar abordagens didáticas. Tesis de doctorado. Universidade de São Paulo.

Karam, R.A.S. y Pietrocola, M. (2009). Habilidades técnicas versus habilidades estruturantes: resolução de problemas e o papel da matemática como estruturante do pensamento físico. Alexandria: Revista de Educação em Ciência e Tecnologia 2(2), 181-205.

Kragh, H. (1990). Dirac: A Scientific Biography. Cambridge: Cambridge University Press.

Paty, M. (2003). The idea of quantity at the origin of the legitimacy of mathematization in physics. Constructivism and Practice: Towards a Social and Historical Epistemology. p-109-135.

Paty, M. (2005). Inteligibilidade racional e historicidade. Estudos Avançados 19(54), 369-390.

Poincaré, H. (2000). El valor de la ciência. Río de Janeiro: Contraponto Editora.

Redish, E. (2006). Problem solving and the use of math in physics courses. En: Conference World View on Physics Education, 21-26 de agosto de 2005. Delhi. Proceedings.

Redish, E.F. y Gupta, A. (2009). Making meaning with math in physics: A semantic analysis. En: D. Raine, C. Hurkett y L. Rogers (ed.). Selected contributions from the GIREP-EPEC & PHEC 2009 International Conference (pp. 244-260).

Tuminaro, J. y Redish, E.F. (2007). Elements of a cognitive model of physics problem solving: Epistemic games. Physical Review Special Topics-Physics Education Research, 3(2), 1-22.

Uhden, O.; Karam, R.; Pietrocola, M. y Pospiech, G. (2012). Modelling mathematical reasoning in physics education. Science & Education 21(4), 485-506.